If you’re a regular reader of my blog you’ll know that I’ve spent some time dabbling with neural networks. As I explained here, I’ve used neural networks in my own research to develop inference into causation. Neural networks fall under two general categories that describe their intended use. Supervised neural networks (e.g., multilayer feed-forward networks) are generally used for prediction, whereas unsupervised networks (e.g., Kohonen self-organizing maps) are used for pattern recognition. This categorization partially describes the role of the analyst during model development. For example, a supervised network is developed from a set of known variables and the end goal of the model is to match the predicted output values with the observed via ‘supervision’ of the training process by the analyst. Development of unsupervised networks are conducted independently from the analyst in the sense that the end product is not known and no direct supervision is required to ensure expected or known results are obtained. Although my research objectives were not concerned specifically with prediction, I’ve focused entirely on supervised networks given the number of tools that have been developed to gain insight into causation. Most of these tools have been described in the primary literature but are not available in R.
My previous post on neural networks described a plotting function that can be used to visually interpret a neural network. Variables in the layers are labelled, in addition to coloring and thickening of weights between the layers. A general goal of statistical modelling is to identify the relative importance of explanatory variables for their relation to one or more response variables. The plotting function is used to portray the neural network in this manner, or more specifically, it plots the neural network as a neural interpretation diagram (NID)1. The rationale for use of an NID is to provide insight into variable importance by visually examining the weights between the layers. For example, input (explanatory) variables that have strong positive associations with response variables are expected to have many thick black connections between the layers. This qualitative interpretation can be very challenging for large models, particularly if the sign of the weights switches after passing the hidden layer. I have found the NID to be quite useless for anything but the simplest models.
The weights that connect variables in a neural network are partially analogous to parameter coefficients in a standard regression model and can be used to describe relationships between variables. That is, the weights dictate the relative influence of information that is processed in the network such that input variables that are not relevant in their correlation with a response variable are suppressed by the weights. The opposite effect is seen for weights assigned to explanatory variables that have strong, positive associations with a response variable. An obvious difference between a neural network and a regression model is that the number of weights is excessive in the former case. This characteristic is advantageous in that it makes neural networks very flexible for modeling non-linear functions with multiple interactions, although interpretation of the effects of specific variables is of course challenging.
A method proposed by Garson 19912 (also Goh 19953) identifies the relative importance of explanatory variables for specific response variables in a supervised neural network by deconstructing the model weights. The basic idea is that the relative importance (or strength of association) of a specific explanatory variable for a specific response variable can be determined by identifying all weighted connections between the nodes of interest. That is, all weights connecting the specific input node that pass through the hidden layer to the specific response variable are identified. This is repeated for all other explanatory variables until the analyst has a list of all weights that are specific to each input variable. The connections are tallied for each input node and scaled relative to all other inputs. A single value is obtained for each explanatory variable that describes the relationship with response variable in the model (see the appendix in Goh 1995 for a more detailed description). The original algorithm presented in Garson 1991 indicated relative importance as the absolute magnitude from zero to one such the direction of the response could not be determined. I modified the approach to preserve the sign, as you’ll see below.
We start by creating a neural network model (using the nnet package) from simulated data before illustrating use of the algorithm. The model is created from eight input variables, one response variable, 10000 observations, and an arbitrary correlation matrix that describes relationships between the explanatory variables. A set of randomly chosen parameters describe the relationship of the response variable with the explanatory variables.
require(clusterGeneration)
require(nnet)
#define number of variables and observations
set.seed(2)
num.vars<-8
num.obs<-10000
#define correlation matrix for explanatory variables
#define actual parameter values
cov.mat<-genPositiveDefMat(num.vars,covMethod=c("unifcorrmat"))$Sigma
rand.vars<-mvrnorm(num.obs,rep(0,num.vars),Sigma=cov.mat)
parms<-runif(num.vars,-10,10)
y<-rand.vars %*% matrix(parms) + rnorm(num.obs,sd=20)
#prep data and create neural network
y<-data.frame((y-min(y))/(max(y)-min(y)))
names(y)<-'y'
rand.vars<-data.frame(rand.vars)
mod1<-nnet(rand.vars,y,size=8,linout=T)
The function for determining relative importance is called gar.fun and can be imported from my Github account (gist 6206737). The function reverse depends on the plot.nnet function to get the model weights.
#import 'gar.fun' from Github
source_url('https://gist.githubusercontent.com/fawda123/6206737/raw/d6f365c283a8cae23fb20892dc223bc5764d50c7/gar_fun.r')
The function is very simple to implement and has the following arguments:
out.var |
character string indicating name of response variable in the neural network object to be evaluated, only one input is allowed for models with multivariate response |
mod.in |
model object for input created from nnet function |
bar.plot |
logical value indicating if a figure is also created in the output, default T |
x.names |
character string indicating alternative names to be used for explanatory variables in the figure, default is taken from mod.in |
... |
additional arguments passed to the bar plot function |
The function returns a list with three elements, the most important of which is the last element named rel.imp. This element indicates the relative importance of each input variable for the named response variable as a value from -1 to 1. From these data, we can get an idea of what the neural network is telling us about the specific importance of each explanatory for the response variable. Here’s the function in action:
#create a pretty color vector for the bar plot
cols<-colorRampPalette(c('lightgreen','lightblue'))(num.vars)
#use the function on the model created above
par(mar=c(3,4,1,1),family='serif')
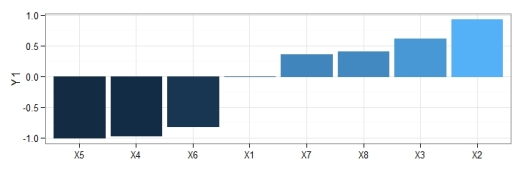
gar.fun('y',mod1,col=cols,ylab='Rel. importance',ylim=c(-1,1))
#output of the third element looks like this
# $rel.imp
# X1 X2 X3 X4 X5
# 0.0000000 0.9299522 0.6114887 -0.9699019 -1.0000000
# X6 X7 X8
# -0.8217887 0.3600374 0.4018899
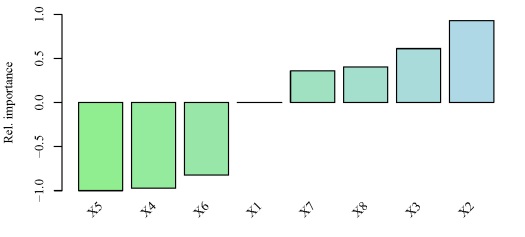
y using the neural network created above. Relative importance was determined using methods in Garson 19912 and Goh 19953. The function can be obtained here.The output from the function and the bar plot tells us that the variables X5 and X2 have the strongest negative and positive relationships, respectively, with the response variable. Similarly, variables that have relative importance close to zero, such as X1, do not have any substantial importance for y. Note that these values indicate relative importance such that a variable with a value of zero will most likely have some marginal effect on the response variable, but its effect is irrelevant in the context of the other explanatory variables.
An obvious question of concern is whether these indications of relative importance provide similar information as the true relationships between the variables we’ve defined above. Specifically, we created the response variable y as a linear function of the explanatory variables based on a set of randomly chosen parameters (parms). A graphical comparison of the indications of relative importance with the true parameter values is as follows:
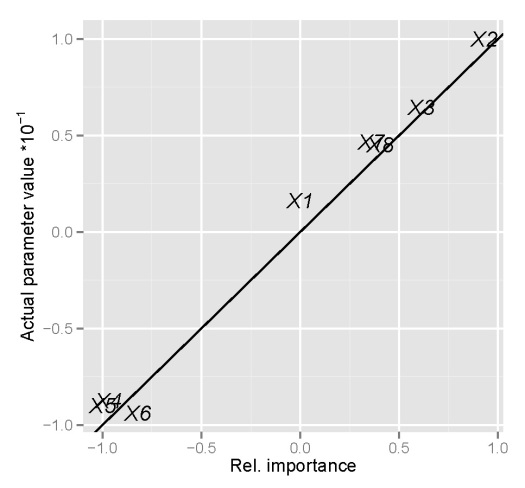
y compared to the true parameter values defined above. Parameter values were divided by ten to facilitate comparison.We assume that concordance between the true parameter values and the indications of relative importance is indicated by similarity between the two, which is exactly what is seen above. We can say with certainty that the neural network model and the function to determine relative importance is providing us with reliable information. A logical question to ask next is whether or not using a neural network provides more insight into variable relationships than a standard regression model, since we know our response variable follows the general form of a linear regression. An interesting exercise could compare this information for a response variable that is more complex than the one we’ve created above, e.g., add quadratic terms, interactions, etc.
As far as I know, Garson’s algorithm has never been modified to preserve the sign of the relationship between variables. This information is clearly more useful than simply examining the magnitude of the relationship, as is the case with the original algorithm. I hope the modified algorithm will be useful for facilitating the use of neural networks to infer causation, although it must be acknowledged that a neural network is ultimately based on correlation and methods that are more heavily based in theory could be more appropriate. Lastly, I consider this blog my contribution to dispelling the myth that neural networks are black boxes (motivated by Olden and Jackson 20024). Useful information can indeed be obtained with the right tools.
-Marcus
1Özesmi, S.L., Özesmi, U. 1999. An artificial neural network approach to spatial habitat modeling with interspecific interaction. Ecological Modelling. 116:15-31.
2Garson, G.D. 1991. Interpreting neural network connection weights. Artificial Intelligence Expert. 6(4):46–51.
3Goh, A.T.C. 1995. Back-propagation neural networks for modeling complex systems. Artificial Intelligence in Engineering. 9(3):143–151.
4Olden, J.D., Jackson, D.A. 2002. Illuminating the ‘black-box’: a randomization approach for understanding variable contributions in artificial neural networks. Ecological Modelling. 154:135-150.
Update:
I’m currently updating all of the neural network functions on my blog to make them compatible with all neural network packages in R. Additionally, the functions will be able to use raw weight vectors as inputs, in addition to model objects as currently implemented. The updates to the gar.fun function include these options. See the examples below for more details. I’ve also changed the plotting to use ggplot2 graphics.
The new arguments for gar.fun are as follows:
out.var |
character string indicating name of response variable in the neural network object to be evaluated, only one input is allowed for models with multivariate response, must be of form ‘Y1’, ‘Y2’, etc. if using numeric values as weight inputs for mod.in |
mod.in |
model object for neural network created using the nnet, RSNNS, or neuralnet packages, alternatively, a numeric vector specifying model weights in specific order, see example |
bar.plot |
logical value indicating if a figure or relative importance values are returned, default T |
struct |
numeric vector of length three indicating structure of the neural network, e.g., 2, 2, 1 for two inputs, two hidden, and one response, only required if mod.in is a vector input |
x.lab |
character string indicating alternative names to be used for explanatory variables in the figure, default is taken from mod.in |
y.lab |
character string indicating alternative names to be used for response variable in the figure, default is taken from out.var |
wts.only |
logical indicating of only model weights should be returned |
# this example shows use of raw input vector as input
# the weights are taken from the nnet model above
# import new function
source_url('https://gist.githubusercontent.com/fawda123/6206737/raw/d6f365c283a8cae23fb20892dc223bc5764d50c7/gar_fun.r')
# get vector of weights from mod1
vals.only <- unlist(gar.fun('y', mod1, wts.only = T))
vals.only
# hidden 1 11 hidden 1 12 hidden 1 13 hidden 1 14 hidden 1 15 hidden 1 16 hidden 1 17
# -1.5440440353 0.4894971240 -0.7846655620 -0.4554819870 2.3803629827 0.4045390778 1.1631255990
# hidden 1 18 hidden 1 19 hidden 1 21 hidden 1 22 hidden 1 23 hidden 1 24 hidden 1 25
# 1.5844070803 -0.4221806079 0.0480375217 -0.3983876761 -0.6046451652 -0.0736146356 0.2176405974
# hidden 1 26 hidden 1 27 hidden 1 28 hidden 1 29 hidden 1 31 hidden 1 32 hidden 1 33
# -0.0906340785 0.1633912108 -0.1206766987 -0.6528977864 1.2255953817 -0.7707485396 -1.0063172490
# hidden 1 34 hidden 1 35 hidden 1 36 hidden 1 37 hidden 1 38 hidden 1 39 hidden 1 41
# 0.0371724519 0.2494350900 0.0220121908 -1.3147089165 0.5753711352 0.0482957709 -0.3368124708
# hidden 1 42 hidden 1 43 hidden 1 44 hidden 1 45 hidden 1 46 hidden 1 47 hidden 1 48
# 0.1253738473 0.0187610286 -0.0612728942 0.0300645103 0.1263138065 0.1542115281 -0.0350399176
# hidden 1 49 hidden 1 51 hidden 1 52 hidden 1 53 hidden 1 54 hidden 1 55 hidden 1 56
# 0.1966119466 -2.7614366991 -0.9671345937 -0.1508876798 -0.2839796515 -0.8379801306 1.0411094014
# hidden 1 57 hidden 1 58 hidden 1 59 hidden 1 61 hidden 1 62 hidden 1 63 hidden 1 64
# 0.7940494280 -2.6602412144 0.7581558506 -0.2997650961 0.4076177409 0.7755417212 -0.2934247464
# hidden 1 65 hidden 1 66 hidden 1 67 hidden 1 68 hidden 1 69 hidden 1 71 hidden 1 72
# 0.0424664179 0.5997626459 -0.3753986118 -0.0021020946 0.2722725781 -0.2353500011 0.0876374693
# hidden 1 73 hidden 1 74 hidden 1 75 hidden 1 76 hidden 1 77 hidden 1 78 hidden 1 79
# -0.0244290095 -0.0026191346 0.0080349427 0.0449513273 0.1577298156 -0.0153099721 0.1960918520
# hidden 1 81 hidden 1 82 hidden 1 83 hidden 1 84 hidden 1 85 hidden 1 86 hidden 1 87
# -0.6892926134 -1.7825068475 1.6225034225 -0.4844547498 0.8954479895 1.1236485983 2.1201674117
# hidden 1 88 hidden 1 89 out 11 out 12 out 13 out 14 out 15
# -0.4196627413 0.4196025359 1.1000994866 -0.0009401206 -0.3623747323 0.0011638613 0.9642290448
# out 16 out 17 out 18 out 19
# 0.0005194378 -0.2682687768 -1.6300590889 0.0021911807
# use the function and modify ggplot object
p1 <- gar.fun('Y1',vals.only, struct = c(8,8,1))
p1
p2 <- p1 + theme_bw() + theme(legend.position = 'none')
p2
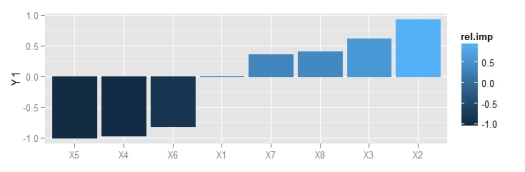
ggplot2 theme.
The user has the responsibility to make sure the weight vector is in the correct order if raw weights are used as input. The function will work if all weights are provided but there is no method for identifying the correct order. The names of the weights in the commented code above describe the correct order, e.g., Hidden 1 11 is the bias layer weight going to hidden node 1, Hidden 1 12 is the first input going to the first hidden node, etc. The first number is an arbitrary place holder indicating the first hidden layer. The correct structure must also be provided for the given length of the input weight vector. NA values should be used if no bias layers are included in the model. Stay tuned for more updates as I continue revising these functions.

Thank you for the post. It is good to find a novel application of neural networks.
Thanks! I plan on having another post or two about additional nnet tools I’ve made. I might even submit them as a package if sufficiently motivated.
Okay, I have to say this, but understand completely that its not the authors fault. AI/Machine Learning/various code type guys have been using the term ‘neural networks’ for years, without anyone pointing out that this a science fiction term ( probably Philip.K.Dick) adopted by philosophers for gedankenexperiment (thought experiments) and used as an ambition for AI. But the Ai versions were never neural networks, because 1. No one has ever figured out how neurons network, and 2. if there are such things, they involve both analog and digital information transmissions .
I bet your ‘neural network’ is devoid of analog. Anyway, philosophy doesn’t own the phrase any more, but its important (I think) to know that even if you are creating AI, you are not mimicking neuronal activity. There, I’ve said it, in a comment that no one will read….
I agree with you completely. I’m not a fan of the term since it’s a gross over-simplification of what it’s meant to represent, as you’ve described. Whenever I present this material I make sure to point out the inappropriate use of the term. I do think that the terminology has, in part, contributed to their overuse and an exaggeration of abilities. All things considered, you have to admit they are a rather clever approach to modelling.
Well, thank you for proving me wrong by both reading, and responding. I do agree that its a very useful approach to modelling, I also agree that this is a valuable contribution to demystifying the approach (a mystery which is probably exaggerated by the use of the term ‘neural’, and thus aggravated by complexity theorists who believe that the right answers ’emerge’ from the process)
Hi. Your graph is great! Is it possible to edit a version for the original garson paper, so without ignoring the signs?
Hi there, I’m not sure what you mean since the current version includes sign of the response. My original code for the function determined relative importance exactly as described in the Garson paper, i.e., only the magnitude of relative importance was included. It’s very easy to modify the source code in my function to only return magnitude. I can update if you’d like.
Hi … Really appreciate the blog posts for giving insights about NN. I am trying to implement this code for variable importance. However, source_gist(‘5086859’) , in the code gives me a connection error. I went to the site where the code is supposed to be stored. But I am not able to access it. Is there a way I can aacess it?? Thanks in anticipation. Also thanks a lot for your blogs
Hi, sorry you couldn’t access the code. I was having trouble with the source function on my last blog post for some reason. You can access the raw code for variable importance here:
Visualizing neural networks in R – update – R is my friend
to me, garson’s algorithm itself seems incorrect. Even though it seems to use the weights from hidden node to the output node, it actually gets cancelled out when it computes the contribution of one input node. for a single input to hidden node contribution calculation, the denominator and numerator both contain the same factor of hidden_to_output node weight value.
I assume the Garson algo described in ref#4 (Olden and Jackson) is correct.
R(a1) = C(a1)/ [C(a1) + C(a2) + C(a3)] and all C(ai) have the common factor W(oa). So R(a1) is independent of W(oa).
Effectively, each input’s importance is independent of the weights from hidden layer to the output.
Is that correct, or am I missing something.
Been a while since I’ve thought about this algorithm… it’s a tricky one. If I’m understanding you correctly, the issue you point out is that the algorithm incorrectly interprets importance in cases where the weights are of opposite sign from input to hidden and hidden to output — the weights cancel out. To me, this isn’t a problem since the weights are determined as a means to minimize prediction error. The weights describe the relationships between input/output that are mediated by the hidden layer. Both sets of weights (I-H, H-O) need to be evaluated to interpret the complex links between input to hidden. I think my figure above provides a useful comparison of relative importance using an independent measure — actual parameter values compared to Garson’s estimates. The two correspond well suggesting the latter is a valid estimate. Please explain if I’ve misinterpreted….
Thanks for looking!
No, it’s not about the sign of the weights. I-H is fine. My concern is about H-O getting cancelled since both numerator C(a1) = W(a1) * W(ao) and denominator [C(a1) + C(a2) + C(a3)] = [W(a1)*W(ao) + W(a3)*W(ao) + W(a3)*W(ao)] have W(ao) common and subsequently, R(a1) = W(a1)/[W(a1) + W(a3) + W(a3)] is independent of weight W(ao) from H-O layer.
Garson uses the abs value |W(a1)*W(ao)| ignoring the sign (so that -ve and +ve correlations are not differentiated) but the factor I mention still cancels out.
Hope this explains my dilemma.
Hi! I’ve been working on an R package with similar goals that you might be interested in. It’s based on an idea Andrew Gelman and Iain Pardoe published in 2007. I’ve put up some examples and things here: http://www.davidchudzicki.com/predcomps/.
The main thing that distinguishes this from other approaches is that it accounts for the distribution of model inputs in a way that other approaches usually don’t.
Another nice feature is that it applies the same way across models (rather than being specifically for neural networks), so it can be helpful in comparing different types of models.
Hi David, I’ll have a look at your package. It seems that these types of tools will be more relevant as we continue to use models with arbitrary structures. I haven’t tested it extensively, but my post on sensitivity analyses describes a function that should work with any model that has a predict method.
Thanks. I enjoyed the sensitivity analysis post. I think there’s a problem with the default settings (setting the variables that aren’t varying to their quantiles):
For example, if we’re doing a sensitivity analysis on x3 when x1 and x2 are negatively correlated with mean zero (so that their product is usually negative), and y = x1 x2 x3, then in real life, y will usually be *decreasing* in x3, but the sensitivity analysis that sets x1 and x2 to their quantiles (independently) will show y *increasing* in x3.
This is one example of what I mean when I say that most approaches to variable importance & sensitivity analysis don’t account for the relationships among the input variables.
Yea I think I get what you’re saying. The sensitivity analysis doesn’t account for covariance among explanatory variables so you could get a misleading result by holding them independently at their quantiles. I made a variant of the sensitivity analysis that grouped explanatory variables into clusters and held them constant at their means. This was my attempt at accounting for covariance since the mean values were based on natural groupings among the variables. This still doesn’t account for variation across the range of values, i.e., x2 is decreasing while x3 increases… not sure how to deal with that.
Hi David! Found it very interesting. I am new to implementation of these codes. Could you give an idea how can we use it for neurelnet or nnet output. A code will be appreciated.
First of all, congratulations.
Just one update, the function call that worked for me is:
gar.fun(‘Y’,mod1)
I do believe that the function was updated after this post.
And another detail: if I change the num.vars to a value above 8 (say 10 for example) the plot order gets messed up.
Roberto, thanks for pointing that out. I fixed the function and the order should be correct now.
Medir la importancia de las variables en una red neuronal con R » Análisis y decisión
NeuralNetTools 1.0.0 now on CRAN – R is my friend
Thank you for the post, is very interesting. Please do you have an idea of how to train a neural network with data such as image, audio,video, text etc
Hi Grace, thanks for reading. I only have experience using neural networks for environmental/ecological applications. I do know that neural networks are commonly used in remote sensing, particularly for image classification. You may want to check out some examples from that field. I have not heard of any examples using neural networks to evaluate audio/video/text, but would be interested to hear if you find any neat examples.
Hi Thanks for this interesting work. I however have a problem in plotting the relative importance. my R program returns this error message: Error in gar.fun(“y”, mod2, col = cols, ylab = “Rel. importance”, ylim = c(-1, :
unused arguments (col = cols, ylab = “Rel. importance”, ylim = c(-1, 1)). is it that the three arguments are missing in your function or how should i go about it?
Hi and sorry you’re having issues. I suggest installing the development version of the package and try using the ‘garson’ function. This version will soon be on CRAN.
# install package from GitHub install.packages('devtools') library(devtools) install_github('fawda123/NeuralNetTools') library(NeuralNetTools) # run the examples for the garson function example(garson)Hope that helps.
-Marcus
Hi Hanningtone.
Just one question. I obtain the same error message than you, but I cannot solve it the intructions of beckmw. Did you ge to solve it?
Hi Virginia,
The released version of this function on CRAN no longer accepts the ylim or cols argument. Instead the function returns a ggplot2 object that can be further modified. Try this example…
library(NeuralNetTools) library(nnet) library(ggplot2) mod <- nnet(Y1 ~ X1 + X2 + X3, data = neuraldat, size = 5) cols <- heat.colors(10) garson(mod) + scale_y_continuous('Rel. Importance', limits = c(-1, 1)) + scale_fill_gradientn(colours = cols) + scale_colour_gradientn(colours = cols)Hope that helps.
-Marcus
“I consider this blog my contribution to dispelling the myth that neural networks are black boxes”
That’s great work. However, I don’t see how the claim of neural networks being a black box is refuted. From a Statistics point of view ANNs are a black box approach due to the fact that the analyst doesn’t get to see an actual model (which makes sense since machine learning techniques were meant to be used by machines and not humans).
In theory you can construct a mathematical equation from a neural network and use it to make predictions (I have actually done this). However, this “model” will be extremely complex and impossible to interpret; therefore, useless. You can heuristically infer variable importance from neural networks but the methods that actually do work (such as sensitivity analysis) are not at all related to the model.
Hi Scipio, I generally agree with your comments about these models being fundamentally different from more conventional statistical models. The statement that you quoted is basically my answer to the common opinion that neural networks are only good for predicting responses. I’ve heard many academics complain that they don’t like neural networks because they tell you nothing about the relationship between input/output variables. I like to think that some of the functions in the NeuralNetTools package (which were adapted from others) help describe these relationships from a neural network. This may be particularly useful since neural networks can describe nonlinear, complex relationships quite well.
Hi Marcus. As you say, NNs can describe nonlinear relationships. Does the method by Garson 1991 (or your version of it) take nonlinear relationships into account? Thanks, jO
I would say yes because the Garson method uses the weights from the neural network to assign importance. If these weights describe a non-linear relationship then that should be reflected in the importance estimates as well. Keep in mind though that the Garson method only describes importance as relative magnitude and not by sign.
Hi Marcus
The “weights” method proposed by Garson as you describe it seems very interesting and not too difficult for me but I have 3 to 4 hidden layers. Do you know how to extend the Garson algorithm to more hidden layers and could briefly explain how to do it? I plan to implement it in Matlab.
Hi Helvi,
The original Garson method was created for neural networks with one hidden layer, as you’ve discovered. I would suggest using the ‘Olden’ method which is a more generic version of Garson’s method that can evaluate multiple layers and also preserves the sign of the variable importance. It’s available in the NeuralNetTools package. You can check the code on GitHub if you want to port it over to MatLab. There are several methods written for different object classes in R but they are are all basically the same. For example, check lines 138-164 for the working parts of the algorithm.
Hope that helps.
-Marcus
Hi Marcus
Thanks again for the answer: Unfortunately I have never used R before, so it is a bit tricky for me to port it to Matlab. I have looked at lines 138-164 but it is a bit tricky without the context.
Would it be possible that you could give some pseudocode for the algorithm or perhaps direct Matlab code (if you are familiar with Matlab)? This would be really great.
Hi Helvi, I am not proficient in Matlab so unfortunately I can’t be of much help. I would suggest checking the references in the help files for each function. The olden papers and Goh 1995 provide detailed descriptions about the Garson algorithm. The ‘olden’ algorithm is a bit more straightforward as it’s simply a matrix multiplication of the connection weights between layers (i.e., a summed product). I’m afraid I can’t provide much more help than that – have a look at the references, they should provide some guidance.
-Marcus
Hi Marcus
Sorry for my late reply. Which Olden and Goh paper do you mean for description of Garson’s and Olden’s algorithm? Probably I will try Olden’s algorithm.
They are listed in the help files for each function in the NeuralNetTools package.
Hi Markus
Thanks for the hint. I have now studied Garson’s algorithm. I have 100 input neurons (100 features), three hidden layers with 50 nodes each and an output layer with 2 nodes (2 classes). Using Garsons’s algorithms I will get two values for each feature because I have 2 ouput nodes. That means I’m getting the importance for each feature for both classes. But in the end I just want a single importance value for each feature.
How can this be achieved?
Hi Helvi,
First, are you using Olden’s method? That approach can be used for neural networks with more than one output. For your problem, I’m not sure it’s possible to get a single importance value for a feature that is categorical. I don’t think this is a problem related to the importance function but rather more related to how neural networks treat categorical values. I have never seen a neural network use a single output node for a categorical variable – the models will treat each outcome as a single output node. Conceptually, this makes sense because why would you be concerned with the importance of a classification if you don’t care about how the variables are related to each class (i.e., each output node)? Think of a binary classification… wouldn’t you be concerned with variables related to a positive outcome vs variables related to a negative outcome? It seems like you’re trying to ask the question ‘which variables are important to the response variable as a whole’, rather than specific outcomes of the category, which seems odd given the type of data you’re using. Not sure if that helps…
-Marcus
Hi Marcus,
Thank you very much for this post!! It is being very useful in my current work …
I am applying the gar.fun function to my data, and the results are different to the ones when I use the garson function included in the NeuralNetTools package. Comparing both, the second one only offers positive values of relative importance. If I calculate the absolute values of the relative importance obtained with gar.fun and compare them with the values obtained with garson, the results are not the same for each variable. Do you know where the problem can be?
Thanks in advance
Virginia
Hi Virginia,
As you’ve found, I modified the package function since I made this post. Another reader pointed out that my original implementation of the function in this blog was actually more like the ‘olden’ method that is now available in the package. Do you get similar results using the old gar.fun function as compared to the ‘olden’ function? They are similar in that both are based on a matrix multiplication of weight connections.
-Marcus
Thank you very much for your fast reply
Respect to the gar.fun, I have worked with the function of this url
‘https://gist.github.com/fawda123/6206737/raw/2e1bc9cbc48d1a56d2a79dd1d33f414213f5f1b1/gar_fun.r’
And the results were the relative importance of each variable with positive and negative values
If I use the garson function that is inside of the package, the results are absolute values, and are different to the ones of the function gar.fun.
I am not sure if I am using the ‘olden’ version of the package (I have just installed it ), and I do not know either the version of the gar.fun
Do you know which of both functions that I am using would be the most appropriate one?
Hi Virginia,
You should download the development version of the package from the GitHub repository: https://github.com/fawda123/NeuralNetTools The download instructions are on the page. After installing the library and loading in R, you can check to make sure you’ve got the most current version by running
sessionInfo()on the command line – you should see which version of NeuralNetTools is running. Also, check the help files for each function (garson and olden) for more info about what each is doing, including references. Hope that helps.-Marcus
Hi Marcus,
Thanks for this post. I have a small doubt. I am trying to get the relative importance of variables using your gar.fun() but each time when I am trying to train the neural network, I am getting different relative importance of variables. Why the variable importance is changing with each training phase?
As per my understanding, variable importance should remain same irrespective of training phases. Am i missing something? or is there any other generic way.
Thanks in Advance
Saurabh Kumar
Hi Saurabh,
I have two comments about this. First, try installing the development version of the NeuralNetTools package, instructions here. I’ve slightly changed the implementation of the garson method in the development version (it will be on CRAN soon). This might help with the problem. Second, I’ve noticed this about the garson method in general that the results can be relatively unstable depending on the dataset. It’s possible that there are weak links between the variables such that the neural network creates a different solution each time and, therefore, different variable importance indicated by the function. I’ve noticed that it tends to give consistent results between models only for datasets with strong correlations or those with a very large sample size. A potential solution is to use an iterative approach where you train a large number of models with different random starting weights (keep the network architecture the same), save the importance values after each fit, then look at the distribution of importance values across all model fits. I think the caret package can do something like this but you’d have to get fancy with using the garson function with each model. If this is a feature you really want, I suggest opening an issue on the Github page with the request.
-Marcus
Hi Marcus,
Great article and well documented, everything runs like clockwork! One question regarding relative importance of variables (disclaimer: I relatively new to this type of analysis, so please bear with me):
How is the “relative importance” metric different from the output in PCA?
Thanks,
Martin
Hi Martin,
Thanks for your comment. Can you please clarify what you mean by ‘output in PCA’? Are you referring to the explained variance of the eigenvectors from PCA? I suppose the relative importance provided by the garson method has a similar interpretation as that from PCA given that both provide a general measure of how ‘important’ or ‘influential’ a variable is in relation to a set of additional variables, but the two analyses (PCA and neural networks) are used for completely different reasons. I don’t think it’s fair to compare the meaning between the two measures in this context. I interpret the ‘relative importance’ provided by Garson’s algorithm as an indication of association of each input variable to the output variable, similar to a simple correlation coefficient. However, note that the values are relative and do not indicate anything about sign of association. On the other hand, explained variance for axes in a PCA describe the combined variation of multiple variables using synthetic components that are orthogonal to each other. I always thought of it as a condensed summary of independent variables, rather than how variables are related to one or more dependent variables as for neural networks or constrained ordination analyses.
-Marcus
Thank you for the information you provide here.
Is there anyway to make the importance weight to a more “readable/editable” table?
I am planning to use the importance of variable for another analysis.
Hi Aril,
This blog is actually kind of dated now… check out the ‘garson’ function in the NeuralNetTools package on CRAN: https://cran.r-project.org/web/packages/NeuralNetTools/index.html
The newer function returns the importance values as a data frame.
Hope that helps.
-Marcus
Hey thanks for your article! Very helpful! I have a question, how can I let the ggplot show the varbale names instead of the xes on the x-axis? I want to know which variables had an influence and with only xes I cannot tell.
Help is very appreciated! Thank you so much.
Hi Tee, the function takes variable names from the input model, so what you see on the axis is how they are named in the data. You can also see the actual values by setting the bar.plot argument as F.
Thanks for sharing the source code! It worked perfectly. I could use it to find important features in a 3000 x 200 x 3 network, and by plotting the values of top 10 features for each category, the distinction was great! I will use it to find important features (genes in my case) that distinguish three stages of cell. I can then use these genes to understand the specific properties of a state. I have two queries: How can I reference the code (apart from website address?), and second, is there a good cutoff you suggest (>.5 and <-.5)
Thanks!
Hi Sumeet, happy to hear the code worked. I suggest running the analysis with the CRAN released version and use the package citation: citation(‘NeuralNetTools’). I don’t know of any strict guidelines for cutoff but you can use a bootstrap analysis to check the variability in the importance values. For example, try running the analysis several times with random starting weights for the network, then check the variation in the importance values. Check out section 2.3 in Beck et al. 2014. http://dx.doi.org/10.1016/j.ecolind.2014.04.002
-Marcus
Thanks for your article. I found it so interesting. however, i have a problem within running the process. How can i change your data with my own dataset. How can i transfer my dataset into the coding process?
Thanks again
Hi Amir, check out my NeuralNetTools package: https://cran.r-project.org/web/packages/NeuralNetTools/index.html In particular, the garson and olden functions estimate variable importance. The help files for each should provide guidance.
-Marcus
Hi Marcus,
Great blog and content.
Re: “I’m currently updating all of the neural network functions on my blog to make them compatible with all neural network packages in R.”
Looked inside the function and did not notice any reference to GRNN package?
Any plans to include it? Thanks and best regards/Dan/
Hi Dan,
No plans yet, but I always accept pull requests on GitHub: https://github.com/fawda123/NeuralNetTools
There have been a number of neural network packages that have been released on CRAN since I originally developed NeuralNetTools. To date, I think the most widely used packages are those I incorporated in NeuralNetTools. I expect to add updates as others increase in popularity. I just checked the CRAN download logs… nnet, neuralnet, and RSNNS make up about 94% of the total downloads for the neural network packages I know about on CRAN:
library("cranlogs") today <- as.character(as.Date(Sys.time())) pkgs <- c('nnet', 'neuralnet', 'RSNNS', 'FCNN4R', 'AMORE', 'monmlp', 'qrnn', 'grnn') tots <- sapply(pkgs, function(x) { sum(cran_downloads(x, from = '2000-01-01', to = today)$count) }) barplot(tots, ylab = 'Downloads to date')Hello, I used your function and it works great. Can you give me a more detailed explanation regarding the relative importance meaning? I have tested the function with multiple neural network models and it always assigns zero (rel imp) to one of the predictors, however, the predictive power of the nnet drops if I remove that predictor. Why does it says 0 if it’s important to be kept in the model?
Hi Diego,
I suggest using the ‘olden’ function from the NeuralNetTools package: https://github.com/fawda123/NeuralNetTools
The Garson algorithm used here is outdated.
Best,
Marcus
Hi, Thanks for your nice job! I want to classify the gender of crab according to its species, frontallip, rearwidth, length, width and depth. so in my neural network, there are six input nodes, a single hidden layer and one output layer with two nodes. How can I apply Garson’s algorithm or Olden’s algorithm? as the recommended number of output node is one.
Another question is: considering the activation function, can I apply ReLU function instead of sigmoid function?
Hi, you can try using the Olden algorithm in the NeuralNetTools package: https://cran.r-project.org/web/packages/NeuralNetTools/index.html
It provides a more informative measure of variable importance than Garson’s algorithm. The ‘out_var’ argument also lets you choose which output node to evaluate.
For the activation function, I would look at the help files for the neural network method you’re using. Each package provides different options so you’ll have to take a look yourself.
Hello.
Very nice work, really appreciating. It shows the graphical presentation of variable importance, but if we want cumulative weights, i.e. Regression coefficients, then how do we calculate them. For instance, X1 is effecting on Y with -0.5 percent etc.
Best Regards
Javid
Hi Javid, just set the bar.plot argument to FALSE. This returns the values instead of the graph. Also check out the newer version implemented in the package here.
-Marcus
Marcus. Thank You very much for your reply. I need another answer hopefully, I will get it from you. If I want to get R2 (or square) for each variable in the model, then what function I should use. Moreover, I want to develop a matrix of plot with dots. One color of dot shows positive and other shows negative impact in model.
If it is possible then please suggest me.
Many thanks
Javid
Hello, good work! It’s really a great post. Thanks! Now,I’m using the garson function from NeuralNetTools to get variable importance of my network. I wolud like to know what is the range that the function gives. Is it like the old gar.fun version, between [-1,1]? or does it start from 0 to +infinite? I’m saying this because the two versions give me result totally different. Variables which has a negative importance in the old version has became with positive importance in the new one.
Thanks in advance!
Best regards
Anna
Hi Anna,
You should use the garson function from the NeuralNetTools package: https://cran.r-project.org/web/packages/NeuralNetTools/index.html
This version shows the magnitude of importance as positive values only (0 and higher). I think this is the more correct interpretation of the original method. If you want importance as both magnitude and direction you should use the olden function in the same package. Hope that helps.
-Marcus
Could you tell me how to reduce the result of an Olden on the y-axis?
For example, I want to reduce every variables number on graph .
x1 : 80.123 ->8.123
x2: 50.456->5.456
x3 : 30.789->3.789
Which option added in below code is available?
olden(nnet_model)
Oops. Sorry.
x1 : 80.123 ->8.0123
x2: 50.456->5.0456
x3 : 30.789->3.0789
Hi there,
I understand what you are saying but I’m not sure why you would want to do this. The importance values are directly proportional to the magnitudes of the connections between the layers, so it could be considered a form of data manipulation if you alter these values. There is some level of information in the relative values of the importance measurements, so it’s not wise to change the data output.
However… if you really want to, you can change the y-axis scaling with ggplot:
library(NeuralNetTools) library(nnet) library(ggplot2) data(neuraldat) set.seed(123) mod <- nnet(Y1 ~ X1 + X2 + X3, data = neuraldat, size = 5) transfun = function() function(x) x / 10 garson(mod) + scale_y_continuous('Importance', labels = transfun())Is this the same code in the olde method?
The olden method is similar but preserves the direction of the importance values. Check out a full description here: https://www.jstatsoft.org/article/view/v085i11
Hi,
thanks for providing your functions.
I tried to apply the functions plot.net and gar.fun to my unwrapped nnet model from mlr package as well as to your example models, but i get the following error messages:
1. gar.fun with your example nnet model
Error in gar.fun(“y”, mod1, col = cols, ylab = “Rel. importance”, ylim = c(-1, :
unused arguments (col = cols, ylab = “Rel. importance”, ylim = c(-1, 1))
2. plot.nnet with my nnet model
Error in eval(mod.in$call$formula) : object ‘f’ not found
As I am not a pro in in r, do you have an idea why?
Could it be related to differing package versions?
Best wishes,
Max
Ah, just found an answer here on the firs error message.
Hi there, I would try using the plotnet and garson functions from the NeuralNetTools package: https://cran.r-project.org/web/packages/NeuralNetTools/index.html
These functions are more mature than those on these older blog posts.
Hello beckmw. I ran across your variable-importance-in-neural-networks in R-Bloggers and followed it here.
I see your still taking questions, maybe?
If so I would like to know how to get my data frame from a NNet output into this layout you used for the plotting important vars, if its not too much to ask please.
# #define correlation matrix for explanatory variables
–How would my data fit here
# #define actual parameter values
# cov.mat<-genPositiveDefMat(num.vars,covMethod=c("unifcorrmat"))$Sigma
# rand.vars<-mvrnorm(num.obs,rep(0,num.vars),Sigma=cov.mat)
# parms<-runif(num.vars,-10,10)
# y<-rand.vars %*% matrix(parms) + rnorm(num.obs,sd=20)
–How would my data fit here
# #prep data and create neural network
# y<-data.frame((y-min(y))/(max(y)-min(y)))
# names(y)<-'y'
# rand.vars<-data.frame(rand.vars)
# mod1<-nnet(rand.vars,y,size=8,linout=T)
My NNet output table is called modeltb2d1a1
I am using:
modeltb2d1a1 <- caret::train(Autodist2 ~ .,
data=df,
method = "nnet")
FROM tutorial at
https://neuropsychology.github.io/psycho.R/2018/06/25/refdata.html
and my data str() it pulls from looks like this:
str(df)
'data.frame': 55497 obs. of 29 variables:
$ Autodist2 : Factor w/ 2 levels "No","Yes": 2 2 2 2 2 2 2 2 2 2 …
$ PayorID : num -0.408 -1.491 1.052 1.147 -0.527 …
$ ClaimType : Factor w/ 2 levels "1","2": 1 1 1 1 1 1 1 1 1 1 …
$ ProviderID : num -1.064 -0.687 0.286 -2.138 -0.273 …
$ SubgroupID : num -0.737 -0.846 -0.237 -0.119 -0.311 …
$ ProviderTaxID4 : num 0.551 -0.144 -0.557 0.551 -0.113 …
$ ClaimStatus_Accepted : Factor w/ 2 levels "No","Yes": 2 1 1 1 1 1 1 2 1 1 …
$ ClaimStatus_In_Process: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 …
$ ProviderState2 : num -0.981 0.742 0.874 1.272 1.139 …
$ CustomEOPLanguage2 : logi TRUE TRUE TRUE TRUE TRUE TRUE …
$ AdjustmentType2 : logi TRUE TRUE TRUE TRUE TRUE TRUE …
$ ExternalNetworkID2 : logi FALSE FALSE FALSE FALSE FALSE FALSE …
$ typeofbillid2 : logi TRUE TRUE TRUE TRUE TRUE TRUE …
$ edi2 : Factor w/ 2 levels "FALSE","TRUE": 2 2 2 2 2 2 2 2 1 1 …
$ drgcode2 : logi FALSE FALSE FALSE TRUE TRUE TRUE …
$ Appeals2 : Factor w/ 2 levels "FALSE","TRUE": 2 1 2 1 1 1 1 1 2 1 …
$ RestictedPayorID : Factor w/ 2 levels "FALSE","TRUE": 2 1 1 1 1 1 1 2 1 1 .
$ ClaimManagerID3 : logi FALSE TRUE TRUE TRUE TRUE TRUE …
$ TBCat_4 : Factor w/ 2 levels "No","Yes": 1 1 1 1 2 1 1 2 1 1 …
$ TBCat_10 : Factor w/ 2 levels "No","Yes": 2 1 1 1 1 1 1 1 1 1 …
$ TBCat_6 : Factor w/ 2 levels "No","Yes": 1 2 1 1 1 2 1 1 1 1 …
$ TBCat_8 : Factor w/ 2 levels "No","Yes": 1 1 2 1 1 1 2 1 1 1 …
$ TBCat_9 : Factor w/ 2 levels "No","Yes": 1 1 1 2 1 1 1 1 1 2 …
$ TBCat_5 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 2 1 …
$ TBCat_7 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 …
$ TBCat_3 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 …
$ TBCat_2 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 …
$ ProductID_3 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 …
$ ProductID_1 : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 …
– attr(*, "na.action")= 'omit' Named int 1 10 12 20 26 32 38 42 43 50 …
..- attr(*, "names")= chr "1" "10" "12" "20" …
I hope you can help me.
bill.poling@zelis.com
Hi Bill, you will have to extract the final model from the caret data object.
library(caret) library(MASS) library(NeuralNetTools) data(iris) TrainData <- iris[,1:4] TrainClasses <- iris[,5] nnetFit <- train(TrainData, TrainClasses, method = "nnet", preProcess = "range", tuneLength = 2, trace = FALSE, maxit = 100) bestmod <- nnetFit$finalModel olden(bestmod, out_var = 'virginica')OK, thank you for your response beckmw.
Cheers
WHP
I am using gar function:
https://gist.githubusercontent.com/fawda123/6206737/raw/d6f365c283a8cae23fb20892dc223bc5764d50c7/gar_fun.r
And when I run these codes:
library(reshape)
names(y)<-'y'
vals.only <- unlist(gar.fun('y', nnet1, wts.only = T))
vals.only
p1 <- gar.fun('Y1',vals.only, struct = c(25,2,1))
p1
It shows the Relative Importance bar chart but it seems that the X1: XN labels do not update.Any suggestion?
Do the X1: XN are the same names of the variables taken from my nnet model & data_NNETor are they are rename/created via the gar function?
Variable importance for SVM regression and averaged neural networks – GrindSkills